
Función de X en Y: la condición de existencia asegura que de cada elemento sale alguna flecha y la de unicidad que sólo sale una.
En matemáticas, una función, aplicación o mapeo f es una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el codominio) de forma que a cada elemento x del dominio le corresponde un único elemento del codominio f(x). Se denota por:
Comúnmente, el término función se utiliza cuando el codominio son valores numéricos, reales o complejos. Entonces se habla de función real o función compleja mientras que a las funciones entre conjuntos cualesquiera se las denomina aplicaciones.
DEFINICIÓN
Una función puede considerarse como un caso particular de una relación o de correspondencia
matemática. Cada relación o correspondencia de un elemento.

con un (y sólo un)

se denota

en lugar de

Se piden que se cumplan dos condiciones, que son las siguientes:
- Condición de existencia: Todos los elementos de X están relacionados con elementos de Y, es decir,

2. Condición de unicidad: Cada elemento de X está relacionado con un único elemento de Y, es decir, si

Notación y nomenclatura
Al dominio también se le llama conjunto de entrada o conjunto inicial. Se denota por

Clasificación de las funciones
Dados dos conjuntos X, Y, consideremos a todas las posibles aplicaciones (funciones) que pueden formarse entre estos dos conjuntos. Podemos diferenciar los siguientes casos:

- Si a cada imagen le corresponde una única preimagen, inyectiva.
- Si la imagen de la función es igual al codominio, sobreyectiva o suprayectiva.
- Una función que sea inyectiva y sobreyectiva simultáneamente, se denomina biyectiva .
Puede haber funciones que sean biyectivas, inyectivas pero no suprayectivas, supreyectiva pero no inyectiva o que no se cumple ninguna de esas condiciones, en cuyo caso no tiene un nombre especifico.
'Definiciones alternas: sea




 dada y sea b un elemento cualquiera del codominio Y. Consideremos la ecuación.
dada y sea b un elemento cualquiera del codominio Y. Consideremos la ecuación.
- la función es suprayectiva o sobreyectiva si, y sólo si, la ecuación siempre tiene al menos una solución.
- la función es inyectiva si, y 'solo si, la ecuación (*) tiene a lo más una solución.
- la función es biyectiva cuando, y sólo cuando, es inyectiva y suprayectiva a la vez.
Aplicación inyectiva y no sobreyectiva
En una función inyectiva, cada elemento imagen tiene única preimágen. Un función que no sea inyectiva, tendrá al menos dos elementos diferentes del dominio que tienen la mis
ma imagen.
En una función suprayectiva (sobreyectiva) cada elemento del codominio es imagen de algún elemento del dominio. Una función no será suprayectiva, cuando al menos un elemento del codominio (conjunto final) no tenga una preimagen.
En el diagrama de Ve corresponden a las aplicaciones que pertenecen a A y no pertenecen a B, esto es las que pertenecen a la diferencia de A y B: A-B.
En estas aplicaciones la cardinalidad de X es siempre menor que la de Y, esto es el conjunto Y tendrá mayor número de elementos que X cuando tratamos de compararlos.
Ejemplo
en el diagrama de la figura:
- todos los elementos de Y, que tienen origen, tienen un único origen, esto hace que la aplicación sea inyectiva
- el elemento d de Y, no tiene ningún origen por lo que esta aplicación no es sobreyectiva.
Segundo ejemplo
Partiendo del conjunto de pinceles con pintura de colores: |  |
 | 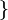 |
Asociando cada pincel con la cara correspondiente:
Dado que cada pincel tiene una cara y solo una cara de su color esta correspondencia es una aplicación, como las caras que tiene pincel de su color, tienen un solo pincel de su color, la aplicación es inyectiva, y como la cara pintada de amarillo, no tiene ningún pincel de este color, la aplicación no es sobreyectiva.
Aplicación no inyectiva y sobreyectiva
Una aplicación no inyectiva tiene al menos un elemento imagen que tiene dos o más orígenes y una sobreyectiva todos los elementos del conjunto final tienen al menos un elemento origen.
En el diagrama de Venn corresponden a las aplicaciones que no pertenecen a A y si pertenecen a B, esto es las que pertenecen a la diferencia de B y A: B-A.
Para esta aplicación el conjunto X ha de tener mayor número de elementos que Y, la cardinalidad de X ha de ser mayor que la de Y.
Ejemplo
en el diagrama de la figura:
- el elemento c de Y, tiene dos orígenes: el 3 y el 4, por lo que esta aplicación no es inyectiva.
- todos los elementos de Y, tienen origen, esto hace que la aplicación sea sobreyectiva.
Segundo ejemplo
Igual que en el ejemplo anterior partiremos del conjunto de pinceles con pintura de colores:
En este caso hay dos pinceles con pintura azul, pero a pasar de tener el mismo color de pintura son dos pinceles distintos.
Como conjunto final tenemos el conjunto de caras pintadas:
Asociando cada pincel con la cara del mismo color, vemos que cada pincel tien
e una cara pintada de su color y solo una, esto hace que la correspondencia sea una aplicación, la cara azul tiene dos pinceles de su mismo color, por lo que no es inyectiva, todas las caras tiene un pincel con su color, luego la aplicación es sobreyectiva.

Aplicación inyectiva y sobreyectiva (biyectiva)
Si una aplicación es inyectiva y sobreyectiva simultáneamente, se denomina biyectiva. Por ser inyectiva los elementos que tienen origen tienen un único origen y por ser sobreyectiva todos los elementos del conjunto final tienen origen.
En el diagrama de Venn el conjunto A es el de las aplicaciones inyectiva y el conjunto B el de las aplicaciones sobreyectiva, las aplicaciones biyectiva, que son inyectiva y sobreyectiva, será la intersección de A y B.
Estas dos circunstancias dan lugar a que el conjunto X e Y tenga
n el mismo número de elementos, la cardinalidad de X e
s la misma que la de Y, esto tiene una gran importancia cuando se pretende comparar dos conjuntos:
- Si dados dos conjuntos podemos encontrar una aplicación biyectiva entre ellos, podemos afirmar, que los dos conjuntos tienen el mismo número de elementos. La cardinalidad de X es igual a la de Y.
Aplicación inyectiva y sobreyectiva (biyectiva)
Si una aplicación es inyectiva y sobreyectiva simultáneamente, se denomina biyectiva. Por ser inyectiva los elementos que tienen origen tienen un único origen y por ser sobreyectiva todos los elementos del conjunto final tienen origen.
En el diagrama de Venn el conjunto A es el de las aplicaciones inyectiva y el conjunto B el de las aplicaciones sobreyectiva, las aplicaciones biyectiva, que son inyectiva y sobreyectiva, será la intersección de A y B.
Estas dos circunstancias dan lugar a que el conjunto X e Y tengan el mismo número de elementos, la cardinalidad de X es la misma que la de Y, esto tiene una gran importancia cuando se pretende comparar dos conjuntos:
- Si dados dos conjuntos podemos encontrar una aplicación biyectiva entre ellos, podemos afirmar, que los dos conjuntos tienen el mismo número de elementos. La cardinalidad de X es igual a la de Y.
Ejemplo
en el diagrama de la figura:
- todos los elementos de Y, que tienen origen, tienen un único origen, esto hace que la aplicación sea inyectiva
- todos los elementos de Y, tienen origen, esto hace que la aplicación sea sobreyectiva.
Si tomaremos por conjunto inicial el conjunto de los números naturales:
y por conjunto final el de los números naturales pares:
Podemos ver que la relación
Por el que a cada número natural x de X, le asociamos un número par 2x de Y, se cumple:
- f: es una aplicación, dado que a cada uno de los valores x de X le corresponde un único valor 2x de Y.
- esta aplicación es inyectiva dado que a cada número par 2x de Y le corresponde un único valor x de X.
- y es sobreyectiva porque todos los números pares tienen un origen
Esto nos permite afirmar que hay el mismo número de números naturales que de números naturales pares, se da la paradoja de que los números naturales pares en un subconjunto propio de los números naturales, esta circunstancia solo se da con los conjuntos infinitos.
Segundo ejemplo
Tomando el conjunto de pinceles como conjunto inicial:
y el de caras como conjunto final:
La correspondencia que asocia cada pincel con la cara de su mismo color es una aplicación porque todos los pinceles tienen una cara con su color y solo una cara de ese color, la aplicación es inyectiva porque un pincel corresponde con una sola cara, y es sobreyectiva porque todas las caras tiene un pincel de su color, al ser inyectiva y sobreyectiva simultáneamente esta aplicación es biyectiva.
Una aplicación biyectiva hace corresponder los elementos del conjunto inicial con los del conjunto final uno a uno, pudiéndose decir que hay el mismo número de elementos en el conjunto inicial que en el final.
Aplicación no inyectiva y no sobreyectiva
Una aplicación no inyectiva tendrá al menos un elemento imagen que tenga dos o más orígenes y una no sobreyectiva tendrá al menos un elemento del conjunto final que no tenga elemento origen. Este tipo de aplicaciones no tiene un nombre especifico y quizá sean las que presenten, desde el punto de vista matemático, un menor interés.
Para esta aplicación los conjuntos X e Y no son comparables, y no podemos plantear ningún supuesto sobre su cardinalidad, partiendo de su comparación, ni sobre su número de elementos.
En el diagrama de Venn corresponden a las aplicaciones que no pertenecen a A y no pertenecen a B, esto es las que no pertenecen a la unión de A y B.
Ejemplo
en el diagrama de la figura:
- el elemento b de Y, tiene dos orígenes: 1 y 2, esto hace que esta aplicación no sea inyectiva
- el elemento a de Y, no tiene ningún origen por lo que esta aplicación no es sobreyectiva
el elemento se obtiene cuando dos funciones con el mismo numerador se conectan de forma biyectiva y no se utiliza en ningún momento la sobreyectiva por medidas de aseguracion la función se emplea de forma rotativa y no se representa en las gráficas.
Segundo ejemplo
Si tomamos como conjunto inicial el de pinceles de colores:
y como conjunto final el de caras coloreadas:
Vemos que todos los pinceles tiene una cara y solo una cara de su mismo color, luego esta correspondencia es una aplicación matemática.
Como la cara azul tiene dos pinceles de su color la aplicación no es inyectiva, y como la cara amarilla no tiene ningún pincel de ese color no es sobreyectiva, luego esta aplicación es no inyectiva y no sobreyectiva.





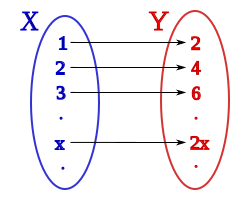






No hay comentarios:
Publicar un comentario