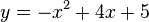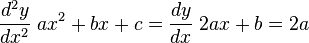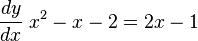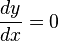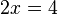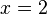Funcion matematica: Funcion Cuadratica

una función cuadrática o función de segundo grado es una función polinómica que se define mediante un polinomio de segundo grado como:

Gráficas de funciones cuadráticas.

$f(x) = ax^2 + bx + c \,$

donde a, b y c son constantes y a es distinto de 0.
La representación gráfica en el plano XY haciendo:

$y = f(x) \,$

esto es:

$y = ax^2 + bx + c \,$

es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de a.

Estudio de la función

Corte con el eje y

La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):

$y = f(0) = a \cdot 0^2 + b \cdot 0 + c \,$

lo que resulta:

$y = f(0) = c \,$

la función corta el eje y en el punto (0, c), siendo c el termino independiente de la función.

Corte con el eje x

La función corta al eje x cuando y vale 0, dada la función:

$y = ax^2 + bx + c \,$

tendremos que:

$y = 0 \quad \longmapsto \quad ax^2 + bx + c = 0 \,$

las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen como es sabido por la expresión:

$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}$

donde:

$b^2 - 4 a c \,$

se le llama discriminante, Δ:

$\Delta = b^2 - 4 a c \,$

según el signo del discriminante podemos distinguir:

Discriminante positivo

Δ > 0, la ecuación tiene dos soluciones, y por tanto la parábola cortara al eje x en dos puntos:

x 1

x 2

Veamos por ejemplo la función:

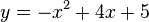
$y = -x^2 + 4x + 5 \,$

que cortara el eje x cuando:

$y = 0 \quad \longmapsto \quad -x^2 + 4x + 5 = 0 \,$

que tendrá por solución general:

$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}$

en este caso:

$x = \frac{-4 \pm \sqrt{4^2 - 4 (-1) 5}}{2 (-1)}$

que resulta:

$x = \frac{-4 \pm \sqrt{16 + 20}}{-2}$

Para esta ecuación el discriminante tiene valor positivo:

$\Delta = 16 + 20 = 36 \,$

y por tanto tiene dos soluciones:

$x_1 = \frac{-4 + \sqrt{36}}{-2} \quad x_2 = \frac{-4 - \sqrt{36}}{-2}$

operando:

$x_1 = \frac{-4 + 6}{-2} \quad x_2 = \frac{-4 - 6}{-2}$

$x_1 = \frac{2}{-2} \quad x_2 = \frac{-10}{-2}$

$x_1 = -1 \quad x_2 = 5$

Los puntos: (-1,0), (5,0) son los de corte con el eje x, como se puede ver en la figura.

Discriminante nulo

Δ = 0, la ecuación tiene una única solución en

x 1

, la parábola solo tiene un punto en común con el eje x, el cual es el vértice de la función donde las dos ramas de la parábola confluyen.

si la función cuadrática:

$y = -x^2 + 4x - 4 \,$

que cortara al eje de las x si:

$y = 0 \quad \longmapsto \quad -x^2 + 4x - 4 = 0 \,$

su solución sera:

$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} \quad x = \frac{-4 \pm \sqrt{4^2 - 4 (-1) (-4)}}{2 (-1)}$

Operando los valores, tendremos:

$x = \frac{-4 \pm \sqrt{4^2 - 16}}{-2} \quad x = \frac{-4 \pm \sqrt{0}}{-2}$

la raíz de cero es cero, luego el discriminante en este caso vale cero, y habrá una única solución:

$x_1 = x_2 = \frac{-4}{-2} = \frac{4}{2} = 2$

El punto de corte de la función con el eje de las x es (2,0), que en este caso es tangencial de la función con el eje, ver figura.

Discriminante negativo

Δ < 0, la ecuación no tiene solución real, y la parábola no corta al eje x.

Si tenemos la función siguiente:

$y = x^2 - 4x - 6 \,$

que corta el eje x cuando:

$y = 0 \quad \longmapsto \quad x^2 - 4x - 6 = 0 \,$

para encontrar su solución haremos:

$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} \quad x = \frac{-4 \pm \sqrt{(-4)^2 - 4 (1) (-6)}}{2 (1)}$

Haciendo las operaciones, tendremos:

$x = \frac{-4 \pm \sqrt{16 - 24}}{2} \quad x = \frac{-4 \pm \sqrt{-8}}{2}$

Al no existir ningún número real que sea la raíz de –8, no se puede continuar haciendo las operaciones, por lo que podemos decir que esta función no tiene corte con el eje x, como se ve en la figura.
Si tenemos en cuente la existencia de los números imaginarios, podemos realizar las siguientes operaciones:

$x = \frac{-4 \pm \sqrt{8(-1)}}{2} \quad x = \frac{-4 \pm \sqrt{8} \, \sqrt{-1}}{2} \quad x = \frac{-4 \pm \sqrt{8} \; i }{2}$

Continuando con las operaciones:

$x = \frac{-4}{2} \pm \frac{\sqrt{8} \; i}{2} \quad x = \frac{-4}{2} \pm \sqrt{\frac{8}{4}} \; i \quad x = -2 \pm \sqrt{2} \; i$

dando como solución:

$x_1 = -2 + \sqrt{2} \; i$

$x_2 = -2 - \sqrt{2} \; i$

Dado el plano cartesiano xy, real, la parábola vista no corta el eje real x en ningún punto, esa misma ecuación estudiada dentro de los números complejos presenta dos soluciones, cumpliéndose de este modo el Teorema fundamental del álgebra.

Extremos relativos

Para localizar los extremos relativos, se calcula la derivada de la función, y se iguala a cero, la solución a esta ecuación son los posibles máximos y mínimos de la función, en este caso, partiendo de la función cuadrática:

$y = ax^2 + bx + c \,$

calculamos su derivada respecto a x:

$\frac{dy}{dx} ax^2 + bx + c = 2ax + b$

que si la igualamos a cero, tenemos:

$2ax + b = 0 \,$

donde x valdrá:

$x = \frac{-b}{2a}$

En la vertical que pasa por este valor de x se encontrar el valor máximo o mínimo relativo de la función.
Para saber si es un máximo o un mínimo es necesario ver la derivada segunda de la función, veamos:

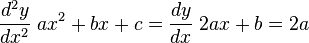
$\frac{d^2y}{dx^2} \; ax^2 + bx + c = \frac{dy}{dx} \; 2ax + b = 2a$

esto es: 2a sera positivo cuando a sea positivo y negativo si a es negativo, por tanto, si la derivada segunda 2a es positiva la parábola es cóncava y el punto será un mínimo de la función, si a es negativa la parábola será convexa y sea un máximo.

Ejemplo 1

Dada la función:

$y = x^2 - x - 2 \,$

De la figura, calcularemos su derivada primera:

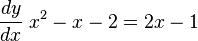
$\frac{dy}{dx} \; x^2 - x - 2 = 2x - 1$

Esta derivada valdrá cero:

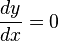
$\frac{dy}{dx} = 0$

cuando:

$2x - 1 = 0 \,$

esto es:

$2x = 1 \,$

$x = \cfrac{1}{2}$

Esta función presenta un extremo relativo para $x = \frac{1}{2}$ , veamos si es un máximo o un mínimo, calculando la derivada segunda:

$\frac{d^2y}{dx^2} \; x^2 - x - 2 = \frac{dy}{dx} \; 2x - 1 = 2$

Que es 2, dado que 2 es un valor positivo, la función es convexa, y el extremo relativo que presente para : $x = \cfrac{1}{2}$ , es un mínimo. El valor de la derivada segunda de una función de segundo grado es el coeficiente de

y = x 2

, por lo que a la vista de la ecuación, podíamos adelantar que seria mínimo sin calcular la derivada segunda.

Ejemplo 2

Dada la función:

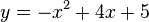
$y = -x^2 + 4x + 5 \,$

Para calcular sus extremos relativos calcularemos su derivada primera:

$\frac{dy}{dx} \; -x^2 + 4x + 5 = -2x + 4$

Esta derivada valdrá cero cuando:

$-2x + 4 = 0 \,$

esto es:

$2x = 4 \,$

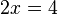
que resulta:

$x = 2 \,$

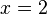
Para

x = 2

, la función presenta un extremo relativo, como sabemos que el coeficiente de

x 2

, es negativo es un máximo, de todas formas se puede calcular la derivada segunda en este punto, comprobando si la función es cóncava o convexa.

Forma factorizada

Toda función cuadrática se puede factorizar en función de sus raíces. Dada:

$f(x) = ax^2 + bx + c \,$

se puede factorizar como:

$f(x) = a(x - x_1)(x - x_2) \,$

siendo a el coeficiente principal de la función, por ello se extrae siempre como factor común, de no escribirse, el coeficiente de

x 2

sería siempre 1.

x 1

x 2

representan las raíces de

f (x)

. En el caso de que el Discriminante Δ sea igual a 0 entonces

x 1 = x 2

por lo que podríamos escribir:

$f(x) = a(x - x_1)^2 \,$

En este caso a

x 1

se la denomina raíz doble, ya que su orden de multiplicidad es 2.

Forma canónica

Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:

$f(x) = a (x - h)^2 + k \,$

A esta forma de expresión se la llama forma canónica. Siendo a el coeficiente principal y el par ordenado (h;k) las coordenadas del vértice de la parábola. Para llegar a esta expresión se parte de la forma polinómica y se realiza el siguiente procedimiento:

Dado:

$f(x) = ax^2 + bx + c \,$

Se extrae a como factor común en el término cuadrático y en el lineal.

$f(x) = a \left ( x^2 + \frac{b}{a} x \right ) + c \,$

Se completa el trinomio cuadrado perfecto, sumando y restando para no alterar la igualdad.

$f(x) = a \left (x^2 + \frac{b}{a} x + \frac{b^2}{4 a^2} \right ) + c - \frac{b^2}{4 a}$

Se factoriza formando el cuadrado de un binomio.

$f(x) = a \left (x + \frac{b}{2a} \right )^2 + c - \frac{b^2}{4a}$

sustituyendo:

$h = \frac{-b}{2a},\ k = c - \frac{b^2}{4a}$

la expresión queda:

$f(x) = a (x - h)^2 + k \,$

Determinar la ecuación conocidos tres puntos.

Partiendo de la forma de la ecuación:

$y = ax^2 +bx +c \,$

y conocidos tres puntos del plano xy por los que pasa una función polinomica de segundo grado:

$(x_1,y_1), \; (x_2,y_2), \; (x_3,y_3)$

se cumplira que:

$\left \{ \begin{matrix} y_1 = ax_{1}^2 +bx_1 +c \\ y_2 = ax_{2}^2 +bx_2 +c \\ y_3 = ax_{3}^2 +bx_3 +c \end{matrix} \right .$

con lo que tenemos un sistema de tres ecuaciones con tres incógnitas, donde las incógnitas son: a, b y c, este sistema tendrá solución si el determinante de los coeficientes de las incógnitas es distinto de cero.

Funcion matematica

Páginas

Funcion Cuadratica

Estudio de la función

Corte con el eje y

Corte con el eje x

Discriminante positivo

Discriminante nulo

Discriminante negativo

Extremos relativos

Ejemplo 1

Ejemplo 2

Forma factorizada

Forma canónica

Determinar la ecuación conocidos tres puntos.

Seguidores

Archivo del blog

Datos personales